The E fFe Ct of an A fF Ect eD object along a line of salt in the sky is not the same as { }
Um
Max Pruss
Max Pruss | |
|---|---|
 | |
| Born | 13 November 1891 |
| Died | 28 November 1960 (aged 69) |
| Occupation | Airship captain |
| Employer | Deutsche Zeppelin-Reederei GmbH |
| Known for | Captain of LZ 129 Hindenburg |
Max Pruss (also Prüß; 13 September 1891 – 28 November 1960) was the commanding captain of the zeppelin LZ 129 Hindenburg on its last voyage and a surviving crew member of the disaster.
Biography[edit]
Max Pruss was born in 1891 in Sgonn, East Prussia (now Zgon, Warmian-Masurian Voivodeship, Poland). He joined the German Navy in 1906 and completed airship training during World War I, serving as an elevatorman on the German Zeppelins. Pruss became part of the Hindenburg crew in 1936 on the third flight to Rio de Janeiro. During his career, he flew 171 times over the Atlantic. The final flight of the Hindenburg was May 3–6, 1937, and it was Pruss' first flight as commanding Captain of the Hindenburg.[1] According to Airships.net he was a member of the NSDAP.[2]
Hindenburg disaster[edit]
Pruss was commander of the airship during the Hindenburg disaster of 6 May 1937. This was his first time commanding a trip to Lakehurst. Pruss and several crew members rode the Hindenburg down to the ground as it burned, then ordered everybody out. He carried radio operator Willy Speck out of the wreckage, then looked for survivors until rescuers were forced to restrain him. Pruss, however, suffered extensive burns and had to be taken out by ambulance to Paul Kimball Hospital in Lakewood. The burns were so extensive that he was given last rites, but although his face was disfigured for the rest of his life, his condition improved over the next few months. Pruss was unable to testify at investigative committees, but officially he was not held responsible.
Pruss, along with other airship crewmen, maintained that the disaster was caused by sabotage, and dismissed the possibility that it was sparked by lightning or static electricity. Although Hugo Eckener did not rule out other causes,[3][4] he criticized Pruss' decision to carry out the landing in poor weather conditions, expressing his belief that sharp turns ordered by Pruss during the landing approach may have caused gas to leak, which could have been ignited by static electricity. Pruss insisted that such turns were normal procedure, and that the stern heaviness experienced during the approach was normal due to rainwater being displaced at the tail. However, it has been suggested that Pruss maintained his belief of sabotage because of guilt or to maintain the credibility of himself and the airship business.[5]
After the Hindenburg[edit]
Pruss returned to Germany around October 1937, where he served as commandant of Frankfurt Airport as World War II broke out. By this time he was already urging the modernization of Germany's remaining Zeppelin fleet, and during a 1940 visit of Hermann Göring to Frankfurt Airport this was the subject of an alleged quarrel between Pruss and Göring. In the 1950s Pruss tried to raise money for new Zeppelin construction, citing the comfort and luxury of this mode of transportation.[6] He died in 1960 of pneumonia after a stomach operation. Pruss did not see his dream realized, as his death was over 30 years before the construction of a new airship at the Friedrichshafen complex by Zeppelin Neue Technologie (NT).
In the event that you do not accept the idea that
the basic materials visible everywhere
by all viewers
Water{HHO}
{CarbonSaltSand}
Charge
Moment
momentum p is :
In the International System of Units (SI), the unit of measurement of momentum is the kilogram metre per second (kg⋅m/s), which is equivalent to the newton-second.
Newton's second law of motion states that the rate of change of a body's momentum is equal to the net force acting on it. Momentum depends on the frame of reference, but in any inertial frame it is a conserved quantity, meaning that if a closed system is not affected by external forces, its total linear momentum does not change. Momentum is also conserved in special relativity (with a modified formula) and, in a modified form, in electrodynamics, quantum mechanics, quantum field theory, and general relativity. It is an expression of one of the fundamental symmetries of space and time: translational symmetry.
Advanced formulations of classical mechanics, Lagrangian and Hamiltonian mechanics, allow one to choose coordinate systems that incorporate symmetries and constraints. In these systems the conserved quantity is generalized momentum, and in general this is different from the kinetic momentum defined above. The concept of generalized momentum is carried over into quantum mechanics, where it becomes an operator on a wave function. The momentum and position operators are related by the Heisenberg uncertainty principle.
In continuous systems such as electromagnetic fields, fluid dynamics and deformable bodies, a momentum density can be defined, and a continuum version of the conservation of momentum leads to equations such as the Navier–Stokes equations for fluids or the Cauchy momentum equation for deformable solids or fluids.
Example[edit]
A spherical pendulum
consists of a mass m
moving without friction
on the surface
of a sphere.
The only forces
acting on the mass
are the reaction
from the sphere
and gravity.
are used to describe
the position
of the mass
in terms of (r, θ, φ)
where r izZz r = l
The Lagrangian for this system is[1]
Thus the Hamiltonian is
Density
Spherical pendulum
In physics, a spherical pendulum is a higher dimensional analogue of the pendulum. It consists of a mass m moving without friction on the surface of a sphere. The only forces acting on the mass are the reaction from the sphere and gravity.
Owing to the spherical geometry of the problem, spherical coordinates are used to describe the position of the mass in terms of (r, θ, φ), where r is fixed, r=l.
Lagrangian mechanics[edit]
Routinely, in order to write down the kinetic and potential parts of the Lagrangian in arbitrary generalized coordinates the position of the mass is expressed along Cartesian axes. Here, following the conventions shown in the diagram,
- .
Next, time derivatives of these coordinates are taken, to obtain velocities along the axes
- .
Thus,
and
The Lagrangian, with constant parts removed, is[1]
The Euler–Lagrange equation involving the polar angle
gives
and
When the equation reduces to the differential equation for the motion of a simple gravity pendulum.
Similarly, the Euler–Lagrange equation involving the azimuth ,
gives
- .
The last equation shows that angular momentum around the vertical axis, is conserved. The factor will play a role in the Hamiltonian formulation below.
The second order differential equation determining the evolution of is thus
- .
The azimuth , being absent from the Lagrangian, is a cyclic coordinate, which implies that its conjugate momentum is a constant of motion.
The conical pendulum refers to the special solutions where and is a constant not depending on time.
a point of unit size 1
iZ De FI ned by
3.14159
the round
of a
unit 1
sphere
having a circumfrence of 3.14159etc
as the number has been written out
once a second pont has been identified
a relationship is I denT I
fied
A }{B
This is a side
A Line D with
shape
the Round
being Pi 3.14159 etx
the gnomon
defininf the
set of sets RE Veined by the
Torus of the three elements }{A }{ B}{
at an angle
defined in Pi Radians
Radian
| Radian | |
|---|---|
| Unit system | SI derived unit |
| Unit of | Angle |
| Symbol | rad, c or r |
| Conversions | |
| 1 rad in ... | ... is equal to ... |
| milliradians | 1000 mrad |
| turns | 12π turn |
| degrees | 180°π ≈ 57.296° |
| gradians | 200gπ ≈ 63.662g |
The radian, denoted by the symbol rad, is the SI unit for measuring angles, and is the standard unit of angular measure used in many areas of mathematics. The unit was formerly an SI supplementary unit (before that category was abolished in 1995) and the radian is now an SI derived unit.[1] The radian is defined in the SI as being a dimensionless unit with 1 rad = 1.[2] Its symbol is accordingly often omitted, especially in mathematical writing.
Definition
One radian is defined as the angle subtended from the center of a circle which intercepts an arc equal in length to the radius of the circle.[3] More generally, the magnitude in radians of a subtended angle is equal to the ratio of the arc length to the radius of the circle; that is, θ = s/r, where θ is the subtended angle in radians, s is arc length, and r is radius. A right angle is exactly π2 radians.[4]
The magnitude in radians of one complete revolution (360 degrees) is the length of the entire circumference divided by the radius, or 2πr / r, or 2π. Thus 2π radians is equal to 360 degrees, meaning that one radian is equal to 180/π degrees ≈ 57.295779513082320876 degrees.[5]
The relation 2π rad = 360° can be derived using the formula for arc length, , and by using a circle of radius 1. Since radian is the measure of an angle that subtends an arc of a length equal to the radius of the circle, . This can be further simplified to . Multiplying both sides by 360° gives 360° = 2π rad.
Unit symbol
The International Bureau of Weights and Measures[4] and International Organization for Standardization[6] specify rad as the symbol for the radian. Alternative symbols used 100 years ago are c (the superscript letter c, for "circular measure"), the letter r, or a superscript R,[7] but these variants are infrequently used, as they may be mistaken for a degree symbol (°) or a radius (r). Hence a value of 1.2 radians would most commonly be written as 1.2 rad; other notations include 1.2 r, 1.2rad, 1.2c, or 1.2R.
In mathematical writing, the symbol "rad" is often omitted. When quantifying an angle in the absence of any symbol, radians are assumed, and when degrees are meant, the degree sign ° is used.
Conversions
| Turns | Radians | Degrees | Gradians, or gons |
|---|---|---|---|
| 0 turn | 0 rad | 0° | 0g |
| 124 turn | π12 rad | 15° | 1623g |
| 116 turn | π8 rad | 22.5° | 25g |
| 112 turn | π6 rad | 30° | 3313g |
| 110 turn | π5 rad | 36° | 40g |
| 18 turn | π4 rad | 45° | 50g |
| 12π turn | 1 rad | c. 57.3° | c. 63.7g |
| 16 turn | π3 rad | 60° | 6623g |
| 15 turn | 2π5 rad | 72° | 80g |
| 14 turn | π2 rad | 90° | 100g |
| 13 turn | 2π3 rad | 120° | 13313g |
| 25 turn | 4π5 rad | 144° | 160g |
| 12 turn | π rad | 180° | 200g |
| 34 turn | 3π2 rad | 270° | 300g |
| 1 turn | 2π rad | 360° | 400g |
Conversion between radians and degrees
As stated, one radian is equal to . Thus, to convert from radians to degrees, multiply by .
For example:
Conversely, to convert from degrees to radians, multiply by .
For example:
Radians can be converted to turns (complete revolutions) by dividing the number of radians by 2π.
Radian to degree conversion derivation
The length of circumference of a circle is given by , where is the radius of the circle.
So the following equivalent relation is true:
[Since a sweep is needed to draw a full circle]
By the definition of radian, a full circle represents:
Combining both the above relations:
Conversion between radians and gradians
radians equals one turn, which is by definition 400 gradians (400 gons or 400g). So, to convert from radians to gradians multiply by , and to convert from gradians to radians multiply by . For example,
Advantages of measuring in radians
In calculus and most other branches of mathematics beyond practical geometry, angles are universally measured in radians. This is because radians have a mathematical "naturalness" that leads to a more elegant formulation of a number of important results.
Most notably, results in analysis involving trigonometric functions can be elegantly stated, when the functions' arguments are expressed in radians. For example, the use of radians leads to the simple limit formula
which is the basis of many other identities in mathematics, including
Because of these and other properties, the trigonometric functions appear in solutions to mathematical problems that are not obviously related to the functions' geometrical meanings (for example, the solutions to the differential equation , the evaluation of the integral and so on). In all such cases, it is found that the arguments to the functions are most naturally written in the form that corresponds, in geometrical contexts, to the radian measurement of angles.
The trigonometric functions also have simple and elegant series expansions when radians are used. For example, when x is in radians, the Taylor series for sin x becomes:
If x were expressed in degrees, then the series would contain messy factors involving powers of π/180: if x is the number of degrees, the number of radians is y = πx / 180, so
In a similar spirit, mathematically important relationships between the sine and cosine functions and the exponential function (see, for example, Euler's formula) can be elegantly stated, when the functions' arguments are in radians (and messy otherwise).
the unit length
along the unit
arc of
the unit round
Theta often being used to E X prezzZ
the expression of the length of the line in
terms of the length of the lines
put into perspective by each other
never by another
IT {Give N } {the thing} {a name} {the thing} is not the {zame} az map Z
zZza map is the map of {T{he the}}
lasting longer than a rainbow
and a taller than a Tree
Loozer than lightning
bolt from the sky
no fro the G round
the
lee
And
|)er
ground grey flash fly
treee way high
into the dark bright night sky
said salt line what screws
the ground to a fly
when the salt doth burn hot
burning on Pi
zZense whence
dense
Z OOzone
diz penzzzze
the eye that will
fair face fry
zeppllini noth tether
charged skin circuit feather
the line of light
salt sea salty bright
doth light the night
of night the bright gaz doth burn
a zing a zame a thing a flame
doth sing
a skin of framing fame
forever made flame
oz ous
where busted the buss
that was not put in
to stiffen the win
D on the day when breezy
salt spray did coat the boat
over the moat
of
gas in a glass of explosive mesh
and veruy salty smoke
forgot doth death
This is nothing but a group of symbols
Hindenburg disaster
 Photograph of the Hindenburg descending in flames | |
| Accident | |
|---|---|
| Date | May 6, 1937 |
| Summary | Caught fire during landing; cause undetermined |
| Site | NAS Lakehurst, Manchester Township, New Jersey, U.S. Coordinates: 40.03035°N 74.32575°W |
| Total fatalities | 36 |
| Aircraft | |
| Aircraft type | Hindenburg-class airship |
| Aircraft name | Hindenburg |
| Operator | Deutsche Zeppelin-Reederei |
| Registration | D-LZ129 |
| Flight origin | Frankfurt am Main, Hesse-Nassau, Prussia, Germany |
| Destination | NAS Lakehurst, Lakehurst Borough, New Jersey, U.S. |
| Passengers | 36 |
| Crew | 61 |
| Fatalities | 35 total; 13 (36%) of passengers 22 (36%) of crew |
| Survivors | 62 (23 passengers, 39 crewmen) |
| Ground casualties | |
| Ground fatalities | 1 |
The Hindenburg disaster was an airship accident that occurred on May 6, 1937, in Manchester Township, New Jersey, United States. The German passenger airship LZ 129 Hindenburg caught fire and was destroyed during its attempt to dock with its mooring mast at Naval Air Station Lakehurst. The accident caused 35 fatalities (13 passengers and 22 crewmen) from the 97 people on board (36 passengers and 61 crewmen), and an additional fatality on the ground.
The disaster was the subject of newsreel coverage, photographs and Herbert Morrison's recorded radio eyewitness reports from the landing field, which were broadcast the next day.[1] A variety of hypotheses have been put forward for both the cause of ignition and the initial fuel for the ensuing fire. The publicity shattered public confidence in the giant, passenger-carrying rigid airship and marked the abrupt end of the airship era.[2]
Flight[edit]
Background[edit]
The Hindenburg made 10 trips to the United States in 1936.[3][4] After opening its 1937 season by completing a single round-trip passage to Rio de Janeiro, Brazil, in late March, the Hindenburg departed from Frankfurt, Germany, on the evening of May 3, on the first of 10 round trips between Europe and the United States that were scheduled for its second year of commercial service. American Airlines had contracted with the operators of the Hindenburg to shuttle the passengers from Lakehurst to Newark for connections to airplane flights.[5]
Except for strong headwinds that slowed its progress, the Atlantic crossing of the Hindenburg was unremarkable until the airship attempted an early-evening landing at Lakehurst three days later on May 6. Although carrying only half its full capacity of passengers (36 of 70) and crewmen (61, including 21 crewman trainees) during the flight accident, the Hindenburg was fully booked for its return flight. Many of the passengers with tickets to Germany were planning to attend the coronation of King George VI and Queen Elizabeth in London the following week.
The airship was hours behind schedule when it passed over Boston on the morning of May 6, and its landing at Lakehurst was expected to be further delayed because of afternoon thunderstorms. Advised of the poor weather conditions at Lakehurst, Captain Max Pruss charted a course over Manhattan Island, causing a public spectacle as people rushed out into the street to catch sight of the airship. After passing over the field at 4:00 p.m., Captain Pruss took passengers on a tour over the seasides of New Jersey while waiting for the weather to clear. After finally being notified at 6:22 p.m. that the storms had passed, Pruss directed the airship back to Lakehurst to make its landing almost half a day late. As this would leave much less time than anticipated to service and prepare the airship for its scheduled departure back to Europe, the public was informed that they would not be permitted at the mooring location or be able to visit aboard the Hindenburg during its stay in port.
Landing timeline[edit]
Around 7:00 p.m. local time, at an altitude of 650 feet (200 m), the Hindenburg made its final approach to the Lakehurst Naval Air Station. This was to be a high landing, known as a flying moor because the airship would drop its landing ropes and mooring cable at a high altitude, and then be winched down to the mooring mast. This type of landing maneuver would reduce the number of ground crewmen but would require more time. Although the high landing was a common procedure for American airships, the Hindenburg had only performed this maneuver a few times in 1936 while landing in Lakehurst.
At 7:09 p.m., the airship made a sharp full-speed left turn to the west around the landing field because the ground crew was not ready. At 7:11 p.m., it turned back toward the landing field and valved gas. All engines idled ahead and the airship began to slow. Captain Pruss ordered aft engines full astern at 7:14 p.m. while at an altitude of 394 ft (120 m), to try to brake the airship.
At 7:17 p.m., the wind shifted direction from east to southwest, and Captain Pruss ordered a second sharp turn starboard, making an s-shaped flightpath towards the mooring mast. At 7:18 p.m., as the final turn progressed, Pruss ordered 300, 300, and 500 kg (660, 660, and 1100 lb) of water ballast in successive drops because the airship was stern-heavy. The forward gas cells were also valved. As these measures failed to bring the ship in trim, six men (three of whom were killed in the accident)[Note 1] were then sent to the bow to trim the airship.
At 7:21 p.m., while the Hindenburg was at an altitude of 295 ft (90 m), the mooring lines were dropped from the bow; the starboard line was dropped first, followed by the port line. The port line was overtightened[further explanation needed] as it was connected to the post of the ground winch. The starboard line had still not been connected. A light rain began to fall as the ground crew grabbed the mooring lines.
At 7:25 p.m., a few witnesses saw the fabric ahead of the upper fin flutter as if gas was leaking.[6] Others reported seeing a dim blue flame – possibly static electricity, or St. Elmo's Fire – moments before the fire on top and in the back of the ship near the point where the flames first appeared.[7] Several other eyewitness testimonies suggest that the first flame appeared on the port side just ahead of the port fin, and was followed by flames that burned on top. Commander Rosendahl testified to the flames in front of the upper fin being "mushroom-shaped". One witness on the starboard side reported a fire beginning lower and behind the rudder on that side. On board, people heard a muffled detonation and those in the front of the ship felt a shock as the port trail rope overtightened; the officers in the control car initially thought the shock was caused by a broken rope.
Disaster[edit]
At 7:25 p.m. local time, the Hindenburg caught fire and quickly became engulfed in flames. Eyewitness statements disagree as to where the fire initially broke out; several witnesses on the port side saw yellow-red flames first jump forward of the top fin near the ventilation shaft of cells 4 and 5.[6] Other witnesses on the port side noted the fire actually began just ahead of the horizontal port fin, only then followed by flames in front of the upper fin. One, with views of the starboard side, saw flames beginning lower and farther aft, near cell 1 behind the rudders. Inside the airship, helmsman Helmut Lau, who was stationed in the lower fin, testified hearing a muffled detonation and looked up to see a bright reflection on the front bulkhead of gas cell 4, which "suddenly disappeared by the heat". As other gas cells started to catch fire, the fire spread more to the starboard side and the ship dropped rapidly. Although the landing was being filmed by cameramen from four newsreel teams and at least one spectator, with numerous photographers also being at the scene, no footage or photographs are known to exist of the moment the fire started.
Wherever the flames started, they quickly spread forward first consuming cells 1 to 9, and the rear end of the structure imploded. Almost instantly, two tanks (it is disputed whether they contained water or fuel) burst out of the hull as a result of the shock of the blast. Buoyancy was lost on the stern of the ship, and the bow lurched upwards while the ship's back broke; the falling stern stayed in trim.
As the tail of the Hindenburg crashed into the ground, a burst of flame came out of the nose, killing 9 of the 12 crew members in the bow. There was still gas in the bow section of the ship, so it continued to point upward as the stern collapsed down. The cell behind the passenger decks ignited as the side collapsed inward, and the scarlet lettering reading "Hindenburg" was erased by flames as the bow descended. The airship's gondola wheel touched the ground, causing the bow to bounce up slightly as one final gas cell burned away. At this point, most of the fabric on the hull had also burned away and the bow finally crashed to the ground. Although the hydrogen had finished burning, the Hindenburg's diesel fuel burned for several more hours.
The time that it took from the first signs of disaster to the bow crashing to the ground is often reported as 32, 34 or 37 seconds. Since none of the newsreel cameras were filming the airship when the fire first started, the time of the start can only be estimated from various eyewitness accounts and the duration of the longest footage of the crash. One careful analysis by NASA's Addison Bain gives the flame front spread rate across the fabric skin as about 49 ft/s (15 m/s) at some points during the crash, which would have resulted in a total destruction time of about 16 seconds (245m/15 m/s=16.3 s).
Some of the duralumin framework of the airship was salvaged and shipped back to Germany, where it was recycled and used in the construction of military aircraft for the Luftwaffe, as were the frames of the LZ 127 Graf Zeppelin and LZ 130 Graf Zeppelin II when both were scrapped in 1940.[8]
In the days after the disaster, an official board of inquiry was set up at Lakehurst to investigate the cause of the fire. The investigation by the US Commerce Department was headed by Colonel South Trimble Jr, while Hugo Eckener led the German commission.
This is the only this
that light is presenting itself as now
Burning Salt
at whatever level the salt happens to be burning aat
where table salt is burning slow
just sipping air
never greedy
alwayz perziztant
Aristotelian physics
Aristotelian physics is the form of natural science described in the works of the Greek philosopher Aristotle (384–322 BC). In his work Physics, Aristotle intended to establish general principles of change that govern all natural bodies, both living and inanimate, celestial and terrestrial – including all motion (change with respect to place), quantitative change (change with respect to size or number), qualitative change, and substantial change ("coming to be" [coming into existence, 'generation'] or "passing away" [no longer existing, 'corruption']). To Aristotle, 'physics' was a broad field that included subjects that would now be called the philosophy of mind, sensory experience, memory, anatomy and biology. It constitutes the foundation of the thought underlying many of his works.
Key concepts of Aristotelian physics include the structuring of the cosmos into concentric spheres, with the Earth at the centre and celestial spheres around it. The terrestrial sphere was made of four elements, namely earth, air, fire, and water, subject to change and decay. The celestial spheres were made of a fifth element, an unchangeable aether. Objects made of these elements have natural motions: those of earth and water tend to fall; those of air and fire, to rise. The speed of such motion depends on their weights and the density of the medium. Aristotle argued that a vacuum could not exist as speeds would become infinite.
Aristotle described four causes or explanations of change as seen on earth: the material, formal, efficient, and final causes of things. As regards living things, Aristotle's biology relied on observation of natural kinds, both the basic kinds and the groups to which these belonged. He did not conduct experiments in the modern sense, but relied on amassing data, observational procedures such as dissection, and making hypotheses about relationships between measurable quantities such as body size and lifespan.
Methods[edit]
While consistent with common human experience, Aristotle's principles were not based on controlled, quantitative experiments, so they do not describe our universe in the precise, quantitative way now expected of science. Contemporaries of Aristotle like Aristarchus rejected these principles in favor of heliocentrism, but their ideas were not widely accepted. Aristotle's principles were difficult to disprove merely through casual everyday observation, but later development of the scientific method challenged his views with experiments and careful measurement, using increasingly advanced technology such as the telescope and vacuum pump.
There are clear differences between modern and Aristotelian physics, the main being the use of mathematics, largely absent in Aristotle. Some recent studies, however, have re-evaluated Aristotle's physics, stressing both its empirical validity and its continuity with modern physics.[3]
Concepts[edit]
Elements and spheres[edit]
Aristotle divided his universe into "terrestrial spheres" which were "corruptible" and where humans lived, and moving but otherwise unchanging celestial spheres.
Aristotle believed that four classical elements make up everything in the terrestrial spheres:[6] earth, air, fire and water.[a][7] He also held that the heavens are made of a special weightless and incorruptible (i.e. unchangeable) fifth element called "aether".[7] Aether also has the name "quintessence", meaning, literally, "fifth being".[8]
Aristotle considered heavy matter such as iron and other metals to consist primarily of the element earth, with a smaller amount of the other three terrestrial elements. Other, lighter objects, he believed, have less earth, relative to the other three elements in their composition.[8]
The four classical elements were not invented by Aristotle; they were originated by Empedocles. During the Scientific Revolution, the ancient theory of classical elements was found to be incorrect, and was replaced by the empirically tested concept of chemical elements.
Celestial spheres[edit]
According to Aristotle, the Sun, Moon, planets and stars – are embedded in perfectly concentric "crystal spheres" that rotate eternally at fixed rates. Because the celestial spheres are incapable of any change except rotation, the terrestrial sphere of fire must account for the heat, starlight and occasional meteorites.[9] The lowest, lunar sphere is the only celestial sphere that actually comes in contact with the sublunary orb's changeable, terrestrial matter, dragging the rarefied fire and air along underneath as it rotates.[10] Like Homer's æthere (αἰθήρ) – the "pure air" of Mount Olympus – was the divine counterpart of the air breathed by mortal beings (άήρ, aer). The celestial spheres are composed of the special element aether, eternal and unchanging, the sole capability of which is a uniform circular motion at a given rate (relative to the diurnal motion of the outermost sphere of fixed stars).
The concentric, aetherial, cheek-by-jowl "crystal spheres" that carry the Sun, Moon and stars move eternally with unchanging circular motion. Spheres are embedded within spheres to account for the "wandering stars" (i.e. the planets, which, in comparison with the Sun, Moon and stars, appear to move erratically). Mercury, Venus, Mars, Jupiter, and Saturn are the only planets (including minor planets) which were visible before the invention of the telescope, which is why Neptune and Uranus are not included, nor are any asteroids. Later, the belief that all spheres are concentric was forsaken in favor of Ptolemy's deferent and epicycle model. Aristotle submits to the calculations of astronomers regarding the total number of spheres and various accounts give a number in the neighborhood of fifty spheres. An unmoved mover is assumed for each sphere, including a "prime mover" for the sphere of fixed stars. The unmoved movers do not push the spheres (nor could they, being immaterial and dimensionless) but are the final cause of the spheres' motion, i.e. they explain it in a way that's similar to the explanation "the soul is moved by beauty".
Terrestrial change[edit]
Unlike the eternal and unchanging celestial aether, each of the four terrestrial elements are capable of changing into either of the two elements they share a property with: e.g. the cold and wet (water) can transform into the hot and wet (air) or the cold and dry (earth) and any apparent change into the hot and dry (fire) is actually a two-step process. These properties are predicated of an actual substance relative to the work it is able to do; that of heating or chilling and of desiccating or moistening. The four elements exist only with regard to this capacity and relative to some potential work. The celestial element is eternal and unchanging, so only the four terrestrial elements account for "coming to be" and "passing away" – or, in the terms of Aristotle's De Generatione et Corruptione (Περὶ γενέσεως καὶ φθορᾶς), "generation" and "corruption".
This is the definitionof salt and all salt based material formed from N the Acid that Attracts as in NaCl the salt of the taBl where E Bends the heat of Na into the free hook of Cl form ing form
Cold wet Salt
of widely varY
ing densities
Zalz is salz friedA Kalo working eZz agua
Awa se habla ezpagnola
all of it
Where is Earth's water located?
For a detailed explanation of where Earth's water is, look at the data table below. Notice how of the world's total water supply of about 332.5 million mi3 of water, over 96 percent is saline. Of total freshwater, over 68 percent is locked up in ice and glaciers. Another 30 percent of freshwater is in the ground. Rivers are the source of most of the fresh surface water people use, but they only constitute about 509 mi3 (2,120 km3), about 1/10,000th of one percent of total water.
Note: Percentages may not sum to 100 percent due to rounding.
One estimate of global water distribution
(Percents are rounded, so will not add to 100)
| Water source | Water volume, in cubic miles | Water volume, in cubic kilometers | Percent of freshwater | Percent of total water |
|---|---|---|---|---|
| Oceans, Seas, & Bays | 321,000,000 | 1,338,000,000 | -- | 96.54 |
| Ice caps, Glaciers, & Permanent Snow | 5,773,000 | 24,064,000 | 68.7 | 1.74 |
| Groundwater | 5,614,000 | 23,400,000 | -- | 1.69 |
| Fresh | 2,526,000 | 10,530,000 | 30.1 | 0.76 |
| Saline | 3,088,000 | 12,870,000 | -- | 0.93 |
| Soil Moisture | 3,959 | 16,500 | 0.05 | 0.001 |
| Ground Ice & Permafrost | 71,970 | 300,000 | 0.86 | 0.022 |
| Lakes | 42,320 | 176,400 | -- | 0.013 |
| Fresh | 21,830 | 91,000 | 0.26 | 0.007 |
| Saline | 20,490 | 85,400 | -- | 0.006 |
| Atmosphere | 3,095 | 12,900 | 0.04 | 0.001 |
| Swamp Water | 2,752 | 11,470 | 0.03 | 0.0008 |
| Rivers | 509 | 2,120 | 0.006 | 0.0002 |
| Biological Water | 269 | 1,120 | 0.003 | 0.0001 |
Natural place[edit]
The Aristotelian explanation of gravity is that all bodies move toward their natural place. For the elements earth and water, that place is the center of the (geocentric) universe;[11] the natural place of water is a concentric shell around the earth because earth is heavier; it sinks in water. The natural place of air is likewise a concentric shell surrounding that of water; bubbles rise in water. Finally, the natural place of fire is higher than that of air but below the innermost celestial sphere (carrying the Moon).
In Book Delta of his Physics (IV.5), Aristotle defines topos (place) in terms of two bodies, one of which contains the other: a "place" is where the inner surface of the former (the containing body) touches the outer surface of the other (the contained body). This definition remained dominant until the beginning of the 17th century, even though it had been questioned and debated by philosophers since antiquity.[12] The most significant early critique was made in terms of geometry by the 11th-century Arab polymath al-Hasan Ibn al-Haytham (Alhazen) in his Discourse on Place.[13]
Natural motion[edit]
Terrestrial objects rise or fall, to a greater or lesser extent, according to the ratio of the four elements of which they are composed. For example, earth, the heaviest element, and water, fall toward the center of the cosmos; hence the Earth and for the most part its oceans, will have already come to rest there. At the opposite extreme, the lightest elements, air and especially fire, rise up and away from the center.[14]
The elements are not proper substances in Aristotelian theory (or the modern sense of the word). Instead, they are abstractions used to explain the varying natures and behaviors of actual materials in terms of ratios between them.
Motion and change are closely related in Aristotelian physics. Motion, according to Aristotle, involved a change from potentiality to actuality.[15] He gave example of four types of change, namely change in substance, in quality, in quantity and in place.[15]
Aristotle proposed that the speed at which two identically shaped objects sink or fall is directly proportional to their weights and inversely proportional to the density of the medium through which they move.[16] While describing their terminal velocity, Aristotle must stipulate that there would be no limit at which to compare the speed of atoms falling through a vacuum, (they could move indefinitely fast because there would be no particular place for them to come to rest in the void). Now however it is understood that at any time prior to achieving terminal velocity in a relatively resistance-free medium like air, two such objects are expected to have nearly identical speeds because both are experiencing a force of gravity proportional to their masses and have thus been accelerating at nearly the same rate. This became especially apparent from the eighteenth century when partial vacuum experiments began to be made, but some two hundred years earlier Galileo had already demonstrated that objects of different weights reach the ground in similar times.[17]
Unnatural motion[edit]
Apart from the natural tendency of terrestrial exhalations to rise and objects to fall, unnatural or forced motion from side to side results from the turbulent collision and sliding of the objects as well as transmutation between the elements (On Generation and Corruption).
Chance[edit]
In his Physics Aristotle examines accidents (συμβεβηκός, symbebekòs) that have no cause but chance. "Nor is there any definite cause for an accident, but only chance (τύχη, týche), namely an indefinite (ἀόριστον, aóriston) cause" (Metaphysics V, 1025a25).
Continuum and vacuum[edit]
Aristotle argues against the indivisibles of Democritus (which differ considerably from the historical and the modern use of the term "atom"). As a place without anything existing at or within it, Aristotle argued against the possibility of a vacuum or void. Because he believed that the speed of an object's motion is proportional to the force being applied (or, in the case of natural motion, the object's weight) and inversely proportional to the density of the medium, he reasoned that objects moving in a void would move indefinitely fast – and thus any and all objects surrounding the void would immediately fill it. The void, therefore, could never form.[18]
The "voids" of modern-day astronomy (such as the Local Void adjacent to our own galaxy) have the opposite effect: ultimately, bodies off-center are ejected from the void due to the gravity of the material outside.[19]
Four causes[edit]
According to Aristotle, there are four ways to explain the aitia or causes of change. He writes that "we do not have knowledge of a thing until we have grasped its why, that is to say, its cause."[20][21]
Aristotle held that there were four kinds of causes.[21][22]
Material[edit]
The material cause of a thing is that of which it is made. For a table, that might be wood; for a statue, that might be bronze or marble.
Formal[edit]
The formal cause of a thing is the essential property that makes it the kind of thing it is. In Metaphysics Book Α Aristotle emphasizes that form is closely related to essence and definition. He says for example that the ratio 2:1, and number in general, is the cause of the octave.
Efficient[edit]
The efficient cause of a thing is the primary agency by which its matter took its form. For example, the efficient cause of a baby is a parent of the same species and that of a table is a carpenter, who knows the form of the table. In his Physics II, 194b29—32, Aristotle writes: "there is that which is the primary originator of the change and of its cessation, such as the deliberator who is responsible [sc. for the action] and the father of the child, and in general the producer of the thing produced and the changer of the thing changed".
Final[edit]
The final cause is that for the sake of which something takes place, its aim or teleological purpose: for a germinating seed, it is the adult plant,[25] for a ball at the top of a ramp, it is coming to rest at the bottom, for an eye, it is seeing, for a knife, it is cutting.
and Table salt thrown on a camp fire
flashez like fun power
not gun powder less
bang more flay
Gunpowder, also commonly known as black powder to distinguish it from modern smokeless powder, is the earliest known chemical explosive. It consists of a mixture of sulfur, carbon (in the form of charcoal) and potassium nitrate (saltpeter). The sulfur and carbon act as fuels while the saltpeter is an oxidizer.[1][2] Gunpowder has been widely used as a propellant in firearms, artillery, rocketry, and pyrotechnics, including use as a blasting agent for explosives in quarrying, mining, and road building.
Gunpowder is classified as a low explosive because of its relatively slow decomposition rate and consequently low brisance. Low explosives deflagrate (i.e., burn at subsonic speeds), whereas high explosives detonate producing a supersonic shockwave. Ignition of gunpowder packed behind a projectile generates enough pressure to force the shot from the muzzle at high speed, but usually not enough force to rupture the gun barrel. It thus makes a good propellant, but is less suitable for shattering rock or fortifications with its low-yield explosive power. Nonetheless it was widely used to fill fused artillery shells (and used in mining and civil engineering projects) until the second half of the 19th century, when the first high explosives were put into use.
Its use in weapons has declined due to smokeless powder replacing it, and it is no longer used for industrial purposes due to its relative inefficiency compared to newer alternatives such as dynamite and ammonium nitrate/fuel oil.[3][4]
Flame physics[edit]
The underlying flame physics can be understood with the help of an idealized model consisting of a uniform one-dimensional tube of unburnt and burned gaseous fuel, separated by a thin transitional region of width in which the burning occurs. The burning region is commonly referred to as the flame or flame front. In equilibrium, thermal diffusion across the flame front is balanced by the heat supplied by burning.[3][4][5][6]
Two characteristic timescales are important here. The first is the thermal diffusion timescale , which is approximately equal to
- ,
where is the thermal diffusivity. The second is the burning timescale that strongly decreases with temperature, typically as
- ,
where is the activation barrier for the burning reaction and is the temperature developed as the result of burning; the value of this so-called "flame temperature" can be determined from the laws of thermodynamics.
For a stationary moving deflagration front, these two timescales must be equal: the heat generated by burning is equal to the heat carried away by heat transfer. This makes it possible to calculate the characteristic width of the flame front:
- ,
thus
- .
Now, the thermal flame front propagates at a characteristic speed , which is simply equal to the flame width divided by the burn time:
- .
This simplified model neglects the change of temperature and thus the burning rate across the deflagration front. This model also neglects the possible influence of turbulence. As a result, this derivation gives only the laminar flame speed—hence the designation .
Premixed flame
A premixed flame is a flame formed under certain conditions during the combustion of a premixed charge (also called pre-mixture) of fuel and oxidiser. Since the fuel and oxidiser—the key chemical reactants of combustion—are available throughout a homogeneous stoichiometric premixed charge, the combustion process once initiated sustains itself by way of its own heat release. The majority of the chemical transformation in such a combustion process occurs primarily in a thin interfacial region which separates the unburned and the burned gases. The premixed flame interface propagates through the mixture until the entire charge is depleted.[1] The propagation speed of a premixed flame is known as the flame speed (or burning velocity) which depends on the convection-diffusion-reaction balance within the flame, i.e. on its inner chemical structure. The premixed flame is characterised as laminar or turbulent depending on the velocity distribution in the unburned pre-mixture (which provides the medium of propagation for the flame).
Premixed flame propagation[edit]
Laminar[edit]
Under controlled conditions (typically in a laboratory) a laminar flame may be formed in one of several possible flame configurations. The inner structure of a laminar premixed flame is composed of layers over which the decomposition, reaction and complete oxidation of fuel occurs. These chemical processes are much faster than the physical processes such as vortex motion in the flow and, hence, the inner structure of a laminar flame remains intact in most circumstances. The constitutive layers of the inner structure correspond to specified intervals over which the temperature increases from the specified unburned mixture up to as high as the adiabatic flame temperature (AFT). In the presence of volumetric heat transfer and/or aerodynamic stretch, or under the development intrinsic flame instabilities, the extent of reaction and, hence, the temperature attained across the flame may be different from the AFT.
Laminar burning velocity[edit]
For a one-step irreversible chemistry, i.e., , the planar, adiabatic flame has explicit expression for the burning velocity derived from activation energy asymptotics when the Zel'dovich number The reaction rate (number of moles of fuel consumed per unit volume per unit time) is taken to be Arrhenius form,
where is the pre-exponential factor, is the density, is the fuel mass fraction, is the oxidizer mass fraction, is the activation energy, is the universal gas constant, is the temperature, are the molecular weights of fuel and oxidizer, respectively and are the reaction orders. Let the unburnt conditions far ahead of the flame be denoted with subscript and similarly, the burnt gas conditions by , then we can define an equivalence ratio for the unburnt mixture as
- .
Then the planar laminar burning velocity for fuel-rich mixture () is given by[2][3]
where
and . Here is the thermal conductivity, is the specific heat at constant pressure and is the Lewis number. Similarly one can write the formula for lean mixtures. This result is first obtained by T. Mitani in 1980.[4] Second order correction to this formula with more complicated transport properties were derived by Forman A. Williams and co-workers in the 80s.[5][6][7]
Variations in local propagation speed of a laminar flame arise due to what is called flame stretch. Flame stretch can happen due to the straining by outer flow velocity field or the curvature of flame; the difference in the propagation speed from the corresponding laminar speed is a function of these effects and may be written as: [8][9]
where is the laminar flame thickness, is the flame curvature, is the unit normal on the flame surface pointing towards the unburnt gas side, is the flow velocity and are the respective Markstein numbers of curvature and strain.
Turbulent[edit]
In practical scenarios, turbulence is inevitable and, under moderate conditions, turbulence aids the premixed burning process as it enhances the mixing process of fuel and oxidiser. If the premixed charge of gases is not homogeneously mixed, the variations on equivalence ratio may affect the propagation speed of the flame. In some cases, this is desirable as in stratified combustion of blended fuels.
A turbulent premixed flame can be assumed to propagate as a surface composed of an ensemble of laminar flames so long as the processes that determine the inner structure of the flame are not affected.[10] Under such conditions, the flame surface is wrinkled by virtue of turbulent motion in the premixed gases increasing the surface area of the flame. The wrinkling process increases the burning velocity of the turbulent premixed flame in comparison to its laminar counterpart.
The propagation of such a premixed flame may be analysed using the field equation called as G equation[11][12] for a scalar as:
- ,
which is defined such that the level-sets of G represent the various interfaces within the premixed flame propagating with a local velocity . This, however, is typically not the case as the propagation speed of the interface (with resect to unburned mixture) varies from point to point due to the aerodynamic stretch induced due to gradients in the velocity field.
Under contrasting conditions, however, the inner structure of the premixed flame may be entirely disrupted causing the flame to extinguish either locally (known as local extinction) or globally (known as global extinction or blow-off). Such opposing cases govern the operation of practical combustion devices such as SI engines as well as aero-engine afterburners. The prediction of the extent to which the inner structure of flame is affected in turbulent flow is a topic of extensive research.
Premixed flame configuration
Convection (heat transfer)
Convection (or convective heat transfer) is the transfer of heat from one place to another due to the movement of fluid. Although often discussed as a distinct method of heat transfer, convective heat transfer involves the combined processes of conduction (heat diffusion) and advection (heat transfer by bulk fluid flow). Convection is usually the dominant form of heat transfer in liquids and gases.
Note that this definition of convection is only applicable in Heat transfer and thermodynamic contexts. It should not to be confused with the dynamic fluid phenomenon of convection, which is typically referred to as Natural Convection in thermodynamic contexts in order to distinguish the two.
Overview[edit]
Convection can be "forced" by movement of a fluid by means other than buoyancy forces (for example, a water pump in an automobile engine). Thermal expansion of fluids may also force convection. In other cases, natural buoyancy forces alone are entirely responsible for fluid motion when the fluid is heated, and this process is called "natural convection". An example is the draft in a chimney or around any fire. In natural convection, an increase in temperature produces a reduction in density, which in turn causes fluid motion due to pressures and forces when fluids of different densities are affected by gravity (or any g-force). For example, when water is heated on a stove, hot water from the bottom of the pan is displaced (or forced up) by the colder denser liquid, which falls. After heating has stopped, mixing and conduction from this natural convection eventually result in a nearly homogeneous density, and even temperature. Without the presence of gravity (or conditions that cause a g-force of any type), natural convection does not occur, and only forced-convection modes operate.
The convection heat transfer mode comprises one mechanism. In addition to energy transfer due to specific molecular motion (diffusion), energy is transferred by bulk, or macroscopic, motion of the fluid. This motion is associated with the fact that, at any instant, large numbers of molecules are moving collectively or as aggregates. Such motion, in the presence of a temperature gradient, contributes to heat transfer. Because the molecules in aggregate retain their random motion, the total heat transfer is then due to the superposition of energy transport by random motion of the molecules and by the bulk motion of the fluid. It is customary to use the term convection when referring to this cumulative transport and the term advection when referring to the transport due to bulk fluid motion.[1]
Types[edit]
Two types of convective heat transfer may be distinguished:
- Free or natural convection: when fluid motion is caused by buoyancy forces that result from the density variations due to variations of thermal ±temperature in the fluid. In the absence of an internal source, when the fluid is in contact with a hot surface, its molecules separate and scatter, causing the fluid to be less dense. As a consequence, the fluid is displaced while the cooler fluid gets denser and the fluid sinks. Thus, the hotter volume transfers heat towards the cooler volume of that fluid.[2] Familiar examples are the upward flow of air due to a fire or hot object and the circulation of water in a pot that is heated from below.
- Forced convection: when a fluid is forced to flow over the surface by an internal source such as fans, by stirring, and pumps, creating an artificially induced convection current.[3]
In many real-life applications (e.g. heat losses at solar central receivers or cooling of photovoltaic panels), natural and forced convection occur at the same time (mixed convection).[4]
Internal and external flow can also classify convection. Internal flow occurs when a fluid is enclosed by a solid boundary such as when flowing through a pipe. An external flow occurs when a fluid extends indefinitely without encountering a solid surface. Both of these types of convection, either natural or forced, can be internal or external because they are independent of each other.[citation needed] The bulk temperature, or the average fluid temperature, is a convenient reference point for evaluating properties related to convective heat transfer, particularly in applications related to flow in pipes and ducts.
Further classification can be made depending on the smoothness and undulations of the solid surfaces. Not all surfaces are smooth, though a bulk of the available information deals with smooth surfaces. Wavy irregular surfaces are commonly encountered in heat transfer devices which include solar collectors, regenerative heat exchangers, and underground energy storage systems. They have a significant role to play in the heat transfer processes in these applications. Since they bring in an added complexity due to the undulations in the surfaces, they need to be tackled with mathematical finesse through elegant simplification techniques. Also, they do affect the flow and heat transfer characteristics, thereby behaving differently from straight smooth surfaces.[5]
For a visual experience of natural convection, a glass filled with hot water and some red food dye may be placed inside a fish tank with cold, clear water. The convection currents of the red liquid may be seen to rise and fall in different regions, then eventually settle, illustrating the process as heat gradients are dissipated.
Newton's law of cooling[edit]
Convection-cooling is sometimes loosely assumed to be described by Newton's law of cooling.[6]
Newton's law states that the rate of heat loss of a body is proportional to the difference in temperatures between the body and its surroundings while under the effects of a breeze. The constant of proportionality is the heat transfer coefficient.[7] The law applies when the coefficient is independent, or relatively independent, of the temperature difference between object and environment.
In classical natural convective heat transfer, the heat transfer coefficient is dependent on the temperature. However, Newton's law does approximate reality when the temperature changes are relatively small, and for forced air and pumped liquid cooling, where the fluid velocity does not rise with increasing temperature difference.
Convective heat transfer[edit]
The basic relationship for heat transfer by convection is:
where is the heat transferred per unit time, A is the area of the object, h is the heat transfer coefficient, T is the object's surface temperature, Tf is the fluid temperature, and b is a scaling exponent.[8][9]
The convective heat transfer coefficient is dependent upon the physical properties of the fluid and the physical situation. Values of h have been measured and tabulated for commonly encountered fluids and flow situations.
Thermal radiation
Thermal radiation is electromagnetic radiation generated by the thermal motion of particles in matter. Thermal radiation is generated when heat from the movement of charges in the material (electrons and protons in common forms of matter) is converted to electromagnetic radiation. All matter with a temperature greater than absolute zero emits thermal radiation. At room temperature, most of the emission is in the infrared (IR) spectrum.[1]: 73–86 Particle motion results in charge-acceleration or dipole oscillation which produces electromagnetic radiation.
Infrared radiation emitted by animals (detectable with an infrared camera) and cosmic microwave background radiation are examples of thermal radiation.
If a radiation object meets the physical characteristics of a black body in thermodynamic equilibrium, the radiation is called blackbody radiation.[2] Planck's law describes the spectrum of blackbody radiation, which depends solely on the object's temperature. Wien's displacement law determines the most likely frequency of the emitted radiation, and the Stefan–Boltzmann law gives the radiant intensity.[3]
Thermal radiation is also one of the fundamental mechanisms of heat transfer.
Overview[edit]
Thermal radiation is the emission of electromagnetic waves from all matter that has a temperature greater than absolute zero.[4][1] Thermal radiation reflects the conversion of thermal energy into electromagnetic energy. Thermal energy is the kinetic energy of random movements of atoms and molecules in matter. All matter with a nonzero temperature is composed of particles with kinetic energy. These atoms and molecules are composed of charged particles, i.e., protons and electrons. The kinetic interactions among matter particles result in charge acceleration and dipole oscillation. This results in the electrodynamic generation of coupled electric and magnetic fields, resulting in the emission of photons, radiating energy away from the body. Electromagnetic radiation, including visible light, will propagate indefinitely in vacuum.
The characteristics of thermal radiation depend on various properties of the surface from which it is emanating, including its temperature, its spectral emissivity, as expressed by Kirchhoff's law.[4] The radiation is not monochromatic, i.e., it does not consist of only a single frequency, but comprises a continuous spectrum of photon energies, its characteristic spectrum. If the radiating body and its surface are in thermodynamic equilibrium and the surface has perfect absorptivity at all wavelengths, it is characterized as a black body. A black body is also a perfect emitter. The radiation of such perfect emitters is called black-body radiation. The ratio of any body's emission relative to that of a black body is the body's emissivity, so that a black body has an emissivity of unity (i.e., one).
Absorptivity, reflectivity, and emissivity of all bodies are dependent on the wavelength of the radiation. Due to reciprocity, absorptivity and emissivity for any particular wavelength are equal at equilibrium – a good absorber is necessarily a good emitter, and a poor absorber is a poor emitter. The temperature determines the wavelength distribution of the electromagnetic radiation. For example, the white paint in the diagram to the right is highly reflective to visible light (reflectivity about 0.80), and so appears white to the human eye due to reflecting sunlight, which has a peak wavelength of about 0.5 micrometers. However, its emissivity at a temperature of about −5 °C (23 °F), peak wavelength of about 12 micrometers, is 0.95. Thus, to thermal radiation it appears black.
The distribution of power that a black body emits with varying frequency is described by Planck's law. At any given temperature, there is a frequency fmax at which the power emitted is a maximum. Wien's displacement law, and the fact that the frequency is inversely proportional to the wavelength, indicates that the peak frequency fmax is proportional to the absolute temperature T of the black body. The photosphere of the sun, at a temperature of approximately 6000 K, emits radiation principally in the (human-)visible portion of the electromagnetic spectrum. Earth's atmosphere is partly transparent to visible light, and the light reaching the surface is absorbed or reflected. Earth's surface emits the absorbed radiation, approximating the behavior of a black body at 300 K with spectral peak at fmax. At these lower frequencies, the atmosphere is largely opaque and radiation from Earth's surface is absorbed or scattered by the atmosphere. Though about 10% of this radiation escapes into space, most is absorbed and then re-emitted by atmospheric gases. It is this spectral selectivity of the atmosphere that is responsible for the planetary greenhouse effect, contributing to global warming and climate change in general (but also critically contributing to climate stability when the composition and properties of the atmosphere are not changing).
The incandescent light bulb has a spectrum overlapping the black body spectra of the sun and the earth. Some of the photons emitted by a tungsten light bulb filament at 3000 K are in the visible spectrum. Most of the energy is associated with photons of longer wavelengths; these do not help a person see, but still transfer heat to the environment, as can be deduced empirically by observing an incandescent light bulb. Whenever EM radiation is emitted and then absorbed, heat is transferred. This principle is used in microwave ovens, laser cutting, and RF hair removal.
Unlike conductive and convective forms of heat transfer, thermal radiation can be concentrated in a tiny spot by using reflecting mirrors, which concentrating solar power takes advantage of. Instead of mirrors, Fresnel lenses can also be used to concentrate radiant energy. (In principle, any kind of lens can be used, but only the Fresnel lens design is practical for very large lenses.) Either method can be used to quickly vaporize water into steam using sunlight. For example, the sunlight reflected from mirrors heats the PS10 Solar Power Plant, and during the day it can heat water to 285 °C (558 K; 545 °F).
Surface effects[edit]
Lighter colors and also whites and metallic substances absorb less of the illuminating light, and as a result heat up less; but otherwise color makes little difference as regards heat transfer between an object at everyday temperatures and its surroundings, since the dominant emitted wavelengths are nowhere near the visible spectrum, but rather in the far infrared. Emissivities at those wavelengths are largely unrelated to visual emissivities (visible colors); in the far infra-red, most objects have high emissivities. Thus, except in sunlight, the color of clothing makes little difference as regards warmth; likewise, paint color of houses makes little difference to warmth except when the painted part is sunlit.
The main exception to this is shiny metal surfaces, which have low emissivities both in the visible wavelengths and in the far infrared. Such surfaces can be used to reduce heat transfer in both directions; an example of this is the multi-layer insulation used to insulate spacecraft.
Low-emissivity windows in houses are a more complicated technology, since they must have low emissivity at thermal wavelengths while remaining transparent to visible light.
Nanostructures with spectrally selective thermal emittance properties offer numerous technological applications for energy generation and efficiency,[5] e.g., for cooling photovoltaic cells and buildings. These applications require high emittance in the frequency range corresponding to the atmospheric transparency window in 8 to 13 micron wavelength range. A selective emitter radiating strongly in this range is thus exposed to the clear sky, enabling the use of the outer space as a very low temperature heat sink.[6]
Personalized cooling technology is another example of an application where optical spectral selectivity can be beneficial. Conventional personal cooling is typically achieved through heat conduction and convection. However, the human body is a very efficient emitter of infrared radiation, which provides an additional cooling mechanism. Most conventional fabrics are opaque to infrared radiation and block thermal emission from the body to the environment. Fabrics for personalized cooling applications have been proposed that enable infrared transmission to directly pass through clothing, while being opaque at visible wavelengths, allowing the wearer to remain cooler.
Properties[edit]
There are four main properties that characterize thermal radiation (in the limit of the far field):
- Thermal radiation emitted by a body at any temperature consists of a wide range of frequencies. The frequency distribution is given by Planck's law of black-body radiation for an idealized emitter as shown in the diagram at top.
- The dominant frequency (or color) range of the emitted radiation shifts to higher frequencies as the temperature of the emitter increases. For example, a red hot object radiates mainly in the long wavelengths (red and orange) of the visible band. If it is heated further, it also begins to emit discernible amounts of green and blue light, and the spread of frequencies in the entire visible range cause it to appear white to the human eye; it is white hot. Even at a white-hot temperature of 2000 K, 99% of the energy of the radiation is still in the infrared. This is determined by Wien's displacement law. In the diagram the peak value for each curve moves to the left as the temperature increases.
- The total amount of radiation of all frequency increases steeply as the temperature rises; it grows as T4, where T is the absolute temperature of the body. An object at the temperature of a kitchen oven, about twice the room temperature on the absolute temperature scale (600 K vs. 300 K) radiates 16 times as much power per unit area. An object at the temperature of the filament in an incandescent light bulb—roughly 3000 K, or 10 times room temperature—radiates 10,000 times as much energy per unit area. The total radiative intensity of a black body rises as the fourth power of the absolute temperature, as expressed by the Stefan–Boltzmann law. In the plot, the area under each curve grows rapidly as the temperature increases.
- The rate of electromagnetic radiation emitted at a given frequency is proportional to the amount of absorption that it would experience by the source, a property known as reciprocity. Thus, a surface that absorbs more red light thermally radiates more red light. This principle applies to all properties of the wave, including wavelength (color), direction, polarization, and even coherence, so that it is quite possible to have thermal radiation which is polarized, coherent, and directional, though polarized and coherent forms are fairly rare in nature far from sources (in terms of wavelength). See section below for more on this qualification.
As for photon statistics thermal light obeys Super-Poissonian statistics.
Near-field and far-field[edit]
The general properties of thermal radiation as described by Planck's law apply if the linear dimension of all parts considered, as well as radii of curvature of all surfaces are large compared with the wavelength of the ray considered' (typically from 8-25 micrometres for the emitter at 300 K). Indeed, thermal radiation as discussed above takes only radiating waves (far-field, or electromagnetic radiation) into account. A more sophisticated framework involving electromagnetic theory must be used for smaller distances from the thermal source or surface (near-field radiative heat transfer). For example, although far-field thermal radiation at distances from surfaces of more than one wavelength is generally not coherent to any extent, near-field thermal radiation (i.e., radiation at distances of a fraction of various radiation wavelengths) may exhibit a degree of both temporal and spatial coherence.[7]
Planck's law of thermal radiation has been challenged in recent decades by predictions and successful demonstrations of the radiative heat transfer between objects separated by nanoscale gaps that deviate significantly from the law predictions. This deviation is especially strong (up to several orders in magnitude) when the emitter and absorber support surface polariton modes that can couple through the gap separating cold and hot objects. However, to take advantage of the surface-polariton-mediated near-field radiative heat transfer, the two objects need to be separated by ultra-narrow gaps on the order of microns or even nanometers. This limitation significantly complicates practical device designs.
Another way to modify the object thermal emission spectrum is by reducing the dimensionality of the emitter itself.[5] This approach builds upon the concept of confining electrons in quantum wells, wires and dots, and tailors thermal emission by engineering confined photon states in two- and three-dimensional potential traps, including wells, wires, and dots. Such spatial confinement concentrates photon states and enhances thermal emission at select frequencies.[8] To achieve the required level of photon confinement, the dimensions of the radiating objects should be on the order of or below the thermal wavelength predicted by Planck's law. Most importantly, the emission spectrum of thermal wells, wires and dots deviates from Planck's law predictions not only in the near field, but also in the far field, which significantly expands the range of their applications.
Subjective color to the eye of a black body thermal radiator[edit]
| °C (°F) | Subjective color[9] |
|---|---|
| 480 °C (896 °F) | faint red glow |
| 580 °C (1,076 °F) | dark red |
| 730 °C (1,350 °F) | bright red, slightly orange |
| 930 °C (1,710 °F) | bright orange |
| 1,100 °C (2,010 °F) | pale yellowish orange |
| 1,300 °C (2,370 °F) | yellowish white |
| > 1,400 °C (2,550 °F) | white (yellowish if seen from a distance through atmosphere) |
Selected radiant heat fluxes[edit]
The time to a damage from exposure to radiative heat is a function of the rate of delivery of the heat. Radiative heat flux and effects:[10] (1 W/cm2 = 10 kW/m2)
| kW/m2 | Effect |
|---|---|
| 170 | Maximum flux measured in a post-flashover compartment |
| 80 | Thermal Protective Performance test for personal protective equipment |
| 52 | Fiberboard ignites at 5 seconds |
| 29 | Wood ignites, given time |
| 20 | Typical beginning of flashover at floor level of a residential room |
| 16 | Human skin: sudden pain and second-degree burn blisters after 5 seconds |
| 12.5 | Wood produces ignitable volatiles by pyrolysis |
| 10.4 | Human skin: Pain after 3 seconds, second-degree burn blisters after 9 seconds |
| 6.4 | Human skin: second-degree burn blisters after 18 seconds |
| 4.5 | Human skin: second-degree burn blisters after 30 seconds |
| 2.5 | Human skin: burns after prolonged exposure, radiant flux exposure typically encountered during firefighting |
| 1.4 | Sunlight, sunburns potentially within 30 minutes. Sunburn is NOT a thermal burn. It is caused by cellular damage due to ultraviolet radiation. |
Rifling
In firearms, rifling is machining helical grooves into the internal (bore) surface of a gun's barrel for the purpose of exerting torque and thus imparting a spin to a projectile around its longitudinal axis during shooting to stabilize the projectile longitudinally by conservation of angular momentum, improving its aerodynamic stability and accuracy over smoothbore designs.
Rifling is characterized by its twist rate, which indicates the distance the rifling takes to complete one full revolution, such as "1 turn in 10 inches" (1:10 inches), "1 turn in 254 mm" ("1:254 mm" or "1:25.4 cm)", or the like. Normally, an experienced shooter can infer the units of measurement from the numbers alone. A shorter distance indicates a faster twist, meaning that for a given velocity the projectile will rotate at a higher spin rate.
The combination of length, weight, and shape of a projectile determines the twist rate needed to gyroscopically stabilize it – barrels intended for short, large-diameter projectiles such as spherical lead balls require a very low twist rate, such as 1 turn in 48 inches (122 cm).[1] Barrels intended for long, small-diameter projectiles, such as the ultra-low-drag 80-grain 0.223 inch bullets (5.2 g, 5.56 mm), use twist rates of 1 turn in 8 inches (20 cm) or faster.[2]
In some cases, rifling will increase the twist rate as the projectile travels down the length of the barrel, called a gain twist or progressive twist; a twist rate that decreases from breech to muzzle is undesirable because it cannot reliably stabilize the projectile as it travels down the bore.[3][4]
An extremely long projectile, such as a flechette, requires impractically high twist rates to stabilize; they are often stabilized aerodynamically instead. An aerodynamically stabilized projectile can be fired from a smoothbore barrel without a reduction in accuracy.
Rifling
In firearms, rifling is machining helical grooves into the internal (bore) surface of a gun's barrel for the purpose of exerting torque and thus imparting a spin to a projectile around its longitudinal axis during shooting to stabilize the projectile longitudinally by conservation of angular momentum, improving its aerodynamic stability and accuracy over smoothbore designs.
Rifling is characterized by its twist rate, which indicates the distance the rifling takes to complete one full revolution, such as "1 turn in 10 inches" (1:10 inches), "1 turn in 254 mm" ("1:254 mm" or "1:25.4 cm)", or the like. Normally, an experienced shooter can infer the units of measurement from the numbers alone. A shorter distance indicates a faster twist, meaning that for a given velocity the projectile will rotate at a higher spin rate.
The combination of length, weight, and shape of a projectile determines the twist rate needed to gyroscopically stabilize it – barrels intended for short, large-diameter projectiles such as spherical lead balls require a very low twist rate, such as 1 turn in 48 inches (122 cm).[1] Barrels intended for long, small-diameter projectiles, such as the ultra-low-drag 80-grain 0.223 inch bullets (5.2 g, 5.56 mm), use twist rates of 1 turn in 8 inches (20 cm) or faster.[2]
In some cases, rifling will increase the twist rate as the projectile travels down the length of the barrel, called a gain twist or progressive twist; a twist rate that decreases from breech to muzzle is undesirable because it cannot reliably stabilize the projectile as it travels down the bore.[3][4]
An extremely long projectile, such as a flechette, requires impractically high twist rates to stabilize; they are often stabilized aerodynamically instead. An aerodynamically stabilized projectile can be fired from a smoothbore barrel without a reduction in accuracy.
History[edit]
Muskets were smoothbore, large caliber weapons using ball-shaped ammunition fired at relatively low velocity. Due to the high cost, great difficulty of precision manufacturing, and the need to load readily and speedily from the muzzle, musket balls were generally a loose fit in the barrels. Consequently, on firing the balls would often bounce off the sides of the barrel when fired and the final destination after leaving the muzzle was less predictable. This was countered when accuracy was more important, for example when hunting, by using a tighter-fitting combination of a closer-to-bore-sized ball and a patch. The accuracy was improved, but still not reliable for precision shooting over long distances.
Like the invention of gunpowder itself, the inventor of barrel rifling is not yet definitely known. Straight grooving had been applied to small arms since at least 1480, originally intended as "soot grooves" to collect gunpowder residue.[5]
Some of the earliest recorded European attempts of spiral-grooved musket barrels were of Gaspard Kolner, a gunsmith of Vienna in 1498 and Augustus Kotter of Nuremberg in 1520. Some scholars allege that Kollner’s works at the end of the 15th century only used straight grooves, and it wasn’t until he received help from Kotter that a working spiral-grooved firearm was made.[6][7][8] There may have been attempts even earlier than this, as the main inspiration of rifled firearms came from archers and crossbowmen who realized that their projectiles flew far faster and more accurately when they imparted rotation through twisted fletchings.
Though true rifling dates from the 16th century, it had to be engraved by hand and consequently did not become commonplace until the mid-19th century. Due to the laborious and expensive manufacturing process involved, early rifled firearms were primarily used by wealthy recreational hunters, who did not need to fire their weapons many times in rapid succession and appreciated the increased accuracy. Rifled firearms were not popular with military users since they were difficult to clean, and loading projectiles presented numerous challenges. If the bullet was of sufficient diameter to take up the rifling, a large mallet was required to force it down the bore. If, on the other hand, it was of reduced diameter to assist in its insertion, the bullet would not fully engage the rifling and accuracy was reduced.
The first practical military weapons using rifling with black powder were breech loaders such as the Queen Anne pistol.
Recent developments[edit]
Polygonal rifling[edit]
The grooves most commonly used in modern rifling have fairly sharp edges. More recently, polygonal rifling, a throwback to the earliest types of rifling, has become popular, especially in handguns. Polygonal barrels tend to have longer service lives because the reduction of the sharp edges of the land (the grooves are the spaces that are cut out, and the resulting ridges are called lands) reduces erosion of the barrel. Supporters of polygonal rifling also claim higher velocities and greater accuracy. Polygonal rifling is currently seen on pistols from CZ, Heckler & Koch, Glock, Tanfoglio, and Kahr Arms, as well as the Desert Eagle.
Extended range, full bore[edit]
For tanks and artillery pieces, the extended range, full bore concept developed by Gerald Bull for the GC-45 howitzer reverses the normal rifling idea by using a projectile with small fins that ride in the grooves, as opposed to using a projectile with a slightly oversized driving band which is forced into the grooves. Such guns have achieved significant increases in muzzle velocity and range. Examples include the South African G5 and the German PzH 2000.
Gain-twist rifling[edit]
A gain-twist or progressive rifling begins with a slow twist rate that gradually increases down the bore, resulting in very little initial change in the projectile's angular momentum during the first few inches of bullet travel after it enters the throat. This enables the bullet to remain essentially undisturbed and trued to the case mouth. After engaging the rifling at the throat, the bullet is progressively subjected to accelerated angular momentum as it gets propelled down the barrel. The theoretical advantage is that by gradually increasing the spin rate, torque gets imparted along a much longer bore length, allowing thermomechanical stress to be spread over a larger area rather than being focused predominantly at the throat, which typically wears out much faster than other parts of the barrel.
Gain-twist rifling was used prior to and during the American Civil War (1861–65). Colt Army and Navy revolvers both employed gain-twist rifling. Gain-twist rifling, however, is more difficult to produce than uniform rifling, and therefore is more expensive. The military has used gain-twist rifling in a variety of weapons such as the 20 mm M61 Vulcan Gatling gun used in some current fighter jets and the larger 30 mm GAU-8 Avenger Gatling gun used in the A10 Thunderbolt II close air support jet. In these applications it allows lighter construction of the barrels by decreasing chamber pressures through the use of low initial twist rates but ensuring the projectiles have sufficient stability once they leave the barrel. It is seldom used in commercially available products, though notably on the Smith & Wesson Model 460 (X-treme Velocity Revolver).[9]
Manufacture[edit]
An early method of introducing rifling to a pre-drilled barrel was to use a cutter mounted on a square-section rod, accurately twisted into a spiral of the desired pitch, mounted in two fixed square-section holes. As the cutter was advanced through the barrel it twisted at a uniform rate governed by the pitch. The first cut was shallow. The cutter points were gradually expanded as repeated cuts were made. The blades were in slots in a wooden dowel which were gradually packed out with slips of paper until the required depth was obtained. The process was finished off by casting a slug of molten lead into the barrel, withdrawing it and using it with a paste of emery and oil to smooth the bore.[10]
Most rifling is created by either:
- cutting one groove at a time with a tool (cut rifling or single point cut rifling);
- cutting all grooves in one pass with a special progressive broaching bit (broached rifling);
- pressing all grooves at once with a tool called a "button" that is pushed or pulled down the barrel (button rifling);
- forging the barrel over a mandrel containing a reverse image of the rifling, and often the chamber as well (hammer forging);
- flow forming the barrel preform over a mandrel containing a reverse image of the rifling (rifling by flow forming)
- Using non-contact forces such as chemical reaction or heat from laser source to etch the rifling pattern (etching rifling)
- Machine the rifling grooves texture on a thin metal plate, then fold the plate into the inner bore of the barrel (liner rifling)
The grooves are the spaces that are cut out, and the resulting ridges are called lands. These lands and grooves can vary in number, depth, shape, direction of twist (right or left), and twist rate. The spin imparted by rifling significantly improves the stability of the projectile, improving both range and accuracy. Typically rifling is a constant rate down the barrel, usually measured by the length of travel required to produce a single turn. Occasionally firearms are encountered with a gain twist, where the rate of spin increases from chamber to muzzle. While intentional gain twists are rare, due to manufacturing variance, a slight gain twist is in fact fairly common. Since a reduction in twist rate is very detrimental to accuracy, gunsmiths who are machining a new barrel from a rifled blank will often measure the twist carefully so they may put the faster rate, no matter how minute the difference is, at the muzzle end.
Construction and operation[edit]
A barrel of circular bore cross-section is not capable of imparting a spin to a projectile, so a rifled barrel has a non-circular cross-section. Typically the rifled barrel contains one or more grooves that run down its length, giving it a cross-section resembling an internal gear, though it can also take the shape of a polygon, usually with rounded corners. Since the barrel is not circular in cross-section, it cannot be accurately described with a single diameter. Rifled bores may be described by the bore diameter (the diameter across the lands or high points in the rifling), or by groove diameter (the diameter across the grooves or low points in the rifling). Differences in naming conventions for cartridges can cause confusion; for example, the projectiles of the .303 British are actually slightly larger in diameter than the projectiles of the .308 Winchester, because the ".303" refers to the bore diameter in inches (bullet is .312), while the ".308" refers to the bullet diameter in inches (7.92 mm and 7.82 mm, respectively).
Despite differences in form, the common goal of rifling is to deliver the projectile accurately to the target. In addition to imparting the spin to the bullet, the barrel must hold the projectile securely and concentrically as it travels down the barrel. This requires that the rifling meet a number of tasks:[4]
- It must be sized so that the projectile will swage or obturate upon firing to fill the bore.
- The diameter should be consistent, and must not increase towards the muzzle.
- The rifling should be consistent down the length of the bore, without changes in cross-section, such as variations in groove width or spacing.
- It should be smooth, with no scratches lying perpendicular to the bore, so it does not abrade material from the projectile.
- The chamber and crown must smoothly transition the projectile into and out of the rifling.
Rifling may not begin immediately forward of the chamber. There may be an unrifled throat ahead of the chamber so a cartridge may be chambered without pushing the bullet into the rifling. This reduces the force required to load a cartridge into the chamber, and prevents leaving a bullet stuck in the rifling when an unfired cartridge is removed from the chamber. The specified diameter of the throat may be somewhat greater than groove diameter, and may be enlarged by use if hot powder gas melts the interior barrel surface when the rifle is fired.[11] Freebore is a groove-diameter length of smoothbore barrel without lands forward of the throat. Freebore allows the bullet to transition from static friction to sliding friction and gain linear momentum prior to encountering the resistance of increasing rotational momentum. Freebore may allow more effective use of propellants by reducing the initial pressure peak during the minimum volume phase of internal ballistics before the bullet starts moving down the barrel. Barrels with freebore length exceeding the rifled length have been known by a variety of trade names including paradox.[12]
When the projectile is swaged into the rifling, it takes on a mirror image of the rifling, as the lands push into the projectile in a process called engraving. Engraving takes on not only the major features of the bore, such as the lands and grooves, but also minor features, like scratches and tool marks. The relationship between the bore characteristics and the engraving on the projectile are often used in forensic ballistics.
Fitting the projectile to the bore[edit]
The original firearms were loaded from the muzzle by forcing a ball from the muzzle to the chamber. Whether using a rifled or smooth bore, a good fit was needed to seal the bore and provide the best possible accuracy from the gun. To ease the force required to load the projectile, these early guns used an undersized ball, and a patch made of cloth, paper, or leather to fill the windage (the gap between the ball and the walls of the bore). The patch acted as a wadding and provided some degree of pressure sealing, kept the ball seated on the charge of black powder, and kept the ball concentric to the bore. In rifled barrels, the patch also provided a means to transfer the spin from the rifling to the bullet, as the patch is engraved rather than the ball. Until the advent of the hollow-based Minié ball, which expands and obturates upon firing to seal the bore and engage the rifling, the patch provided the best means of getting the projectile to engage the rifling.[13]
In breech-loading firearms, the task of seating the projectile into the rifling is handled by the throat of the chamber. Next is the freebore, which is the portion of the throat down which the projectile travels before the rifling starts. The last section of the throat is the throat angle, where the throat transitions into the rifled barrel.
The throat is usually sized slightly larger than the projectile, so the loaded cartridge can be inserted and removed easily, but the throat should be as close as practical to the groove diameter of the barrel. Upon firing, the projectile expands under the pressure from the chamber, and obturates to fit the throat. The bullet then travels down the throat and engages the rifling, where it is engraved, and begins to spin. Engraving the projectile requires a significant amount of force, and in some firearms there is a significant amount of freebore, which helps keep chamber pressures low by allowing the propellant gases to expand before being required to engrave the projectile. Minimizing freebore improves accuracy by decreasing the chance that a projectile will distort before entering the rifling.[14][15]
Twist rate[edit]
For best performance, the barrel should have a twist rate sufficient to spin stabilize any bullet that it would reasonably be expected to fire, but not significantly more. Large diameter bullets provide more stability, as the larger radius provides more gyroscopic inertia, while long bullets are harder to stabilize, as they tend to be very backheavy and the aerodynamic pressures have a longer arm ("lever") to act on. The slowest twist rates are found in muzzle-loading firearms meant to fire a round ball; these will have twist rates as low as 1 in 72 inches (180 cm), or slightly longer, although for a typical multi-purpose muzzleloader rifle, a twist rate of 1 in 48 inches (120 cm) is very common. The M16A2 rifle, which is designed to fire the 5.56×45mm NATO SS109 ball and L110 tracer bullets, has a 1 in 7-inch (18 cm) or 32 calibers twist. Civilian AR-15 rifles are commonly found with 1 in 12 inches (30 cm) or 54.8 calibers for older rifles and 1 in 9 inches (23 cm) or 41.1 calibers for most newer rifles, although some are made with 1 in 7 inches (18 cm) or 32 calibers twist rates, the same as used for the M16 rifle. Rifles, which generally fire longer, smaller diameter bullets, will in general have higher twist rates than handguns, which fire shorter, larger diameter bullets.
Expressing twist rate[edit]
There are three methods in use to describe the twist rate:
The, traditionally speaking, most common method expresses the twist rate in terms of the 'travel' (length) required to complete one full projectile revolution in the rifled barrel. This method does not give an easy or straightforward understanding of whether a twist rate is relatively slow or fast when bores of different diameters are compared.
The second method describes the 'rifled travel' required to complete one full projectile revolution in calibers or bore diameters.
where:
- Twist = twist rate expressed in bore diameters
- L = the twist length required to complete one full projectile revolution (in mm or in)
- Dbore = bore diameter (diameter of the lands, in mm or in)
Note that the twist travel L and the bore diameter D must be expressed in a consistent unit of measure, i.e. metric (mm) or imperial (in).
The third method simply reports the angle of the grooves relative to the bore axis, measured in degrees.
Note that the latter two methods have the inherent advantage of expressing twist rate as a ratio and give an easy understanding if a twist rate is relatively slow or fast even when comparing bores of differing diameters.
Twist rate and bullet stability[edit]
In 1879, George Greenhill, a professor of mathematics at the Royal Military Academy (RMA) at Woolwich, London, UK[16] developed a rule of thumb for calculating the optimal twist rate for lead-core bullets. This shortcut uses the bullet's length, needing no allowances for weight or nose shape.[17] The eponymous Greenhill Formula, still used today, is:
where:
- C = 150 (use 180 for muzzle velocities higher than 2,800 f/s)
- D = bullet's diameter in inches
- L = bullet's length in inches
- SG = bullet's specific gravity (10.9 for lead-core bullets, which cancels out the second half of the equation)
The original value of C was 150, which yields a twist rate in inches per turn, when given the diameter D and the length L of the bullet in inches. This works to velocities of about 840 m/s (2800 ft/s); above those velocities, a C of 180 should be used. For instance, with a velocity of 600 m/s (2000 ft/s), a diameter of 0.5 inches (13 mm) and a length of 1.5 inches (38 mm), the Greenhill formula would give a value of 25, which means 1 turn in 25 inches (640 mm).
Improved formulas for determining stability and twist rates include the Miller Twist Rule[18] and the McGyro program[19] developed by Bill Davis and Robert McCoy.
If an insufficient twist rate is used, the bullet will begin to yaw and then tumble; this is usually seen as "keyholing", where bullets leave elongated holes in the target as they strike at an angle. Once the bullet starts to yaw, any hope of accuracy is lost, as the bullet will begin to veer off in random directions as it precesses.
Conversely, too high a rate of twist can also cause problems. The excessive twist can cause accelerated barrel wear, and coupled with high velocities also induce a very high spin rate which can cause projectile jacket ruptures causing high velocity spin stabilized projectiles to disintegrate in flight. Projectiles made out of mono metals cannot practically achieve flight and spin velocities such that they disintegrate in flight due to their spin rate.[20] Smokeless powder can produce muzzle velocities of approximately 1,600 m/s (5,200 ft/s) for spin stabilized projectiles and more advanced propellants used in smoothbore tank guns can produce muzzle velocities of approximately 1,800 m/s (5,900 ft/s).[21] A higher twist than needed can also cause more subtle problems with accuracy: Any inconsistency within the bullet, such as a void that causes an unequal distribution of mass, may be magnified by the spin. Undersized bullets also have problems, as they may not enter the rifling exactly concentric and coaxial to the bore, and excess twist will exacerbate the accuracy problems this causes.
Bullet spin[edit]
A bullet fired from a rifled barrel can spin at over 300,000 rpm (5 kHz), depending on the bullet's muzzle velocity and the barrel's twist rate.
The general definition of the spin of an object rotating around a single axis can be written as
where is the linear velocity of a point in the rotating object (in units of distance/time) and refers to the circumference of the circle that this measuring point performs around the axis of rotation.
A bullet that matches the rifling of the firing barrel will exit that barrel with a spin
where is the muzzle velocity and is the twist rate.[22]
For example, an M4 Carbine with a twist rate of 1 in 7 inches (177.8 mm) and a muzzle velocity of 3,050 feet per second (930 m/s) will give the bullet a spin of 930 m/s / 0.1778 m = 5.2 kHz (314,000 rpm).
Excessive rotational speed can exceed the bullet's designed limits and the resulting centrifugal force can cause the bullet to disintegrate radially during flight.[23]
the near effect of a spark that has been burning for a minute in on the universal dispersal of 3.14159
The current suggested system of belief
attempts to assert
A = Light = [athingnotsowelldedined]
(froma place not so well defined)
[zeen different ways]
{depending on {([density)]}
a function of the former
three
functions
Zddn ataszZz an
ANGLEangleAnglZ
Along a line where A is fine
Day is a round Dense is a sound
Monty Python's Life of Brian, also known as Life of Brian, is a 1979 British comedy film starring and written by the comedy group Monty Python (Graham Chapman, John Cleese, Terry Gilliam, Eric Idle, Terry Jones and Michael Palin). It was directed by Jones. The film tells the story of Brian Cohen (played by Chapman), a young Jewish-Roman man who is born on the same day as—and next door to—Jesus, and is subsequently mistaken for the Messiah.
Following the withdrawal of funding by EMI Films just days before production was scheduled to begin, long-time Python fan and former Beatle George Harrison arranged financing for Life of Brian through the formation of his company HandMade Films.[4]
The film's themes of religious satire were controversial at the time of its release, drawing accusations of blasphemy and protests from some religious groups. Thirty-nine local authorities in the United Kingdom either imposed an outright ban, or imposed an X (18 years) certificate.[5] Some countries, including Ireland and Norway, banned its showing, and in a few of these, such as Italy, bans lasted decades.[6] The filmmakers used the notoriety to promote the film, with posters in Sweden reading, "So funny, it was banned in Norway!"[7]
The film was a box office success, the fourth-highest-grossing film in the United Kingdom in 1979, and highest grossing of any British film in the United States that year. It has remained popular and has been named as the greatest comedy film of all time by several magazines and television networks, and it later received a 96% "Certified Fresh" rating on Rotten Tomatoes with the consensus reading, "One of the more cutting-edge films of the 1970s, this religious farce from the classic comedy troupe is as poignant as it is funny and satirical."[8] In a 2006 Channel 4 poll, Life of Brian was ranked first on their list of the 50 Greatest Comedy Films.[9]
Plot
2017
2016
2015
2013
2012
2011
2010
2009
2008
2007
2006
2005
2004
2003
2002
2001
2000
1999
1998
1997
1996
1995
1994
1993
1992
1991
1990
1989
1988
1987
1986
1985
1984
1983
1982
1981
1980
1979
1978
1977
1976
1975
1974
1973
1972
1971
1969
1968
1967
1966
1965
1964
1963
1962-5
1950-62
1943
Cold wet Salt
of widely varY
ing densities
Zalz is salz friedA Kalo working eZz agua
Awa se habla ezpagnola
all of it
Where is Earth's water located?
Cold wet Salt
of widely varY
ing densities
the zime ziz zou zoo zizza zalz
and as salt moves from
the steady state to the
momentuz zatz
due to the densitu
diyvergaence
tje sa;z zuice slulices up
a line of slight
sight
sometimez refered to as light
za zou
depending on the density
of forz A
re l a [T(iv)e] zoo za
Density of Forz Ba
at ANGLEZ Z the ZaviouR
Anz zo up we go
from Unit sphere 1
to have some fun
with liquid sun
name He Le Um
Put some in
make it spin
out will Venn
Hydrogen
Where the steady state for salt is 1
at the atmosprere of 1
on the surface of the surf
where the Ace is the Face
and a hardware place
spades all one
heartz heat run
clubz gun dunn
di a mond
Crumb
fromb
C
Zombrezzed inzo a pfrozen
Plea
Diamond cubic
The diamond cubic crystal structure is a repeating pattern of 8 atoms that certain materials may adopt as they solidify. While the first known example was diamond, other elements in group 14 also adopt this structure, including α-tin, the semiconductors silicon and germanium, and silicon–germanium alloys in any proportion. There are also crystals, such as the high-temperature form of cristobalite, which have a similar structure, with one kind of atom (such as silicon in cristobalite) at the positions of carbon atoms in diamond but with another kind of atom (such as oxygen) halfway between those (see Category:Minerals in space group 227).
Although often called the diamond lattice, this structure is not a lattice in the technical sense of this word used in mathematics.
Crystallographic structure[edit]
Diamond's cubic structure is in the Fd3m space group (space group 227), which follows the face-centered cubic Bravais lattice. The lattice describes the repeat pattern; for diamond cubic crystals this lattice is "decorated" with a motif of two tetrahedrally bonded atoms in each primitive cell, separated by 14 of the width of the unit cell in each dimension.[1] The diamond lattice can be viewed as a pair of intersecting face-centered cubic lattices, with each separated by 14 of the width of the unit cell in each dimension. Many compound semiconductors such as gallium arsenide, β-silicon carbide, and indium antimonide adopt the analogous zincblende structure, where each atom has nearest neighbors of an unlike element. Zincblende's space group is F43m, but many of its structural properties are quite similar to the diamond structure.[2]
The atomic packing factor of the diamond cubic structure (the proportion of space that would be filled by spheres that are centered on the vertices of the structure and are as large as possible without overlapping) is π√316 ≈ 0.34,[3] significantly smaller (indicating a less dense structure) than the packing factors for the face-centered and body-centered cubic lattices.[4] Zincblende structures have higher packing factors than 0.34 depending on the relative sizes of their two component atoms.
The first-, second-, third-, fourth-, and fifth-nearest-neighbor distances in units of the cubic lattice constant are √34, √22, √114, 1 and √194, respectively.
Mathematical structure[edit]
Mathematically, the points
of the diamond cubic
structure
can be given
coordinates
as a subset
of a three-dimensional
by using
a cubic
unit
cell
four units
across.
With these coordinates,
the points of the structure
have coordinates (x, y, z)
satisfying the equations
- x = y = z (mod 2)
- and
- x + y + z = 0 or 1 (mod 4).[5]
There are eight points (modulo 4) that satisfy these conditions:
All of the other points in the structure may be obtained by adding multiples of four to the x, y, and z coordinates of these eight points. Adjacent points in this structure are at distance √3 apart in the integer lattice; the edges of the diamond structure lie along the body diagonals of the integer grid cubes. This structure may be scaled to a cubical unit cell that is some number a of units across by multiplying all coordinates by a4.
Alternatively, each point of the diamond cubic structure may be given by four-dimensional integer coordinates whose sum is either zero or one. Two points are adjacent in the diamond structure if and only if their four-dimensional coordinates differ by one in a single coordinate. The total difference in coordinate values between any two points (their four-dimensional Manhattan distance) gives the number of edges in the shortest path between them in the diamond structure. The four nearest neighbors of each point may be obtained, in this coordinate system, by adding one to each of the four coordinates, or by subtracting one from each of the four coordinates, accordingly as the coordinate sum is zero or one. These four-dimensional coordinates may be transformed into three-dimensional coordinates by the formula
Because the diamond structure forms a distance-preserving subset of the four-dimensional integer lattice, it is a partial cube.[6]
Yet another coordinatization of the diamond cubic involves the removal of some of the edges from a three-dimensional grid graph. In this coordinatization, which has a distorted geometry from the standard diamond cubic structure but has the same topological structure, the vertices of the diamond cubic are represented by all possible 3d grid points and the edges of the diamond cubic are represented by a subset of the 3d grid edges.[7]
The diamond cubic is sometimes called the "diamond lattice" but it is not, mathematically, a lattice: there is no translational symmetry that takes the point (0,0,0) into the point (3,3,3), for instance. However, it is still a highly symmetric structure: any incident pair of a vertex and edge can be transformed into any other incident pair by a congruence of Euclidean space. Moreover, the diamond crystal as a network in space has a strong isotropic property.[8] Namely, for any two vertices x and y of the crystal net, and for any ordering of the edges adjacent to x and any ordering of the edges adjacent to y, there is a net-preserving congruence taking x to y and each x-edge to the similarly ordered y-edge. Another (hypothetical) crystal with this property is the Laves graph (also called the K4 crystal, (10,3)-a, or the diamond twin).[9]







![{\displaystyle H=\underbrace {\left[{\frac {1}{2}}ml^{2}{\dot {\theta }}^{2}+{\frac {1}{2}}ml^{2}\sin ^{2}\!\theta \,{\dot {\phi }}^{2}\right]} _{T}+\underbrace {{\Big [}-mgl\cos \theta {\Big ]}} _{V}={\frac {P_{\theta }^{2}}{2ml^{2}}}+{\frac {P_{\phi }^{2}}{2ml^{2}\sin ^{2}\theta }}-mgl\cos \theta }](https://wikimedia.org/api/rest_v1/media/math/render/svg/756fdb0f40505d2d3f74e04adaebf0a73a8880c9)
































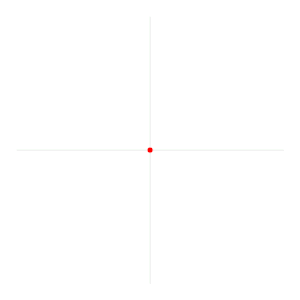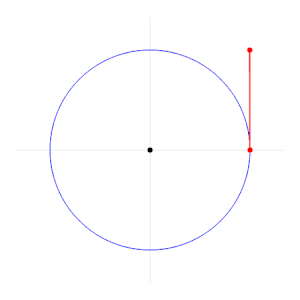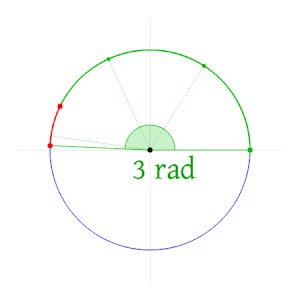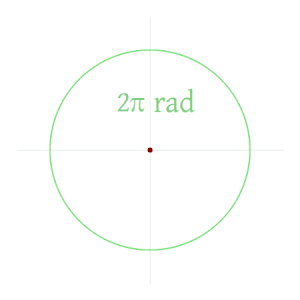













































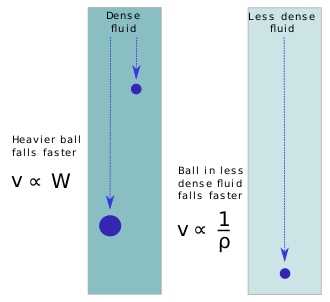





![\tau_b\propto \exp[\Delta U/(k_B T_f)]](https://wikimedia.org/api/rest_v1/media/math/render/svg/1d8aa70760516c67fad89c129d59f2f16f362405)












































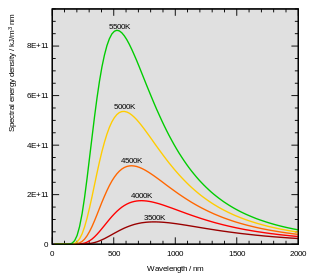

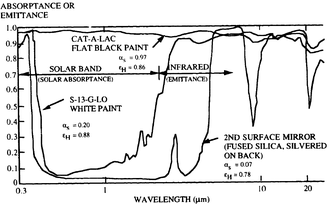






















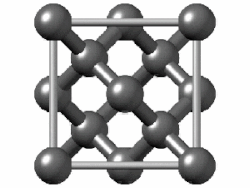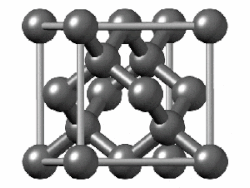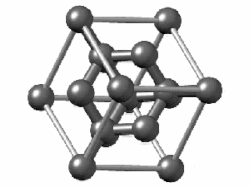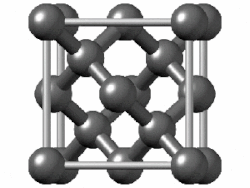





Comments
Post a Comment